XYLENE POWER LTD.

FNR EARTHQUAKE PROTECTION

By Charles Rhodes, P.Eng., Ph.D.

INTRODUCTION:
Elsewhere on this website Fast Neutron Reactors (FNRs) have been identified as the primary source of energy for meeting mankind's future energy needs. This web page focuses on FNR features which prevent earthquake damage.
 

EARTHQUAKE THREAT:
Earthquakes with peak horizontal accelerations of up to 3 g have been known to occur but are extremely rare. Peak horizontal ground accelerations of over 1.26 g seldom occur. If the sodium was completely confined then the sodium pool walls would have to be sufficiently strong to accelerate the entire sodium mass at the peak ground accelertion. That acceleration would impose an extreme hoop stress on the sodium pool steel walls.
 

EARTHQUAKE SOLUTION:
The nuclear island rests on a reinforced concrete foundation baseplate 49 m X 49 m. Hence when there is an earthquake the entire nuclear island move as a single unit with no relative motion between its various solid parts.

The fuel assembly is located deep in the sodium pool. When the sodium pool is shaken there is violent surface wave motion but 6 m down the sodium moves withthe pool walls so there is little relative motion between the sodium and the fuel assembly.

However, the intermediate heat exchange bundles are located near the liquid sodium surface, so they must be secured to the pool walls with violent sodium surface wave motion in mind.

To reduce earthquake induced hoop stress on the sodium pool walls the sodium is permitted to slosh around like water in a half full drinking glass.

In order to allow thermal expansion and contraction of the NaK pipes there is no rigid connection between the intermediate heat exchangers and the sodium pool liner. The reactor space enclosure walls above the sodium pool are attached to the pool deck. These walls are permitted to flex to maintain a gas seal while allowing for thermal expansion and contraction of the NaK piping.. There is a small gap between the bottom of the reactor space enclosure side wall and the pool deck so that the wall can thermally expand with respect to the pool deck. This gap is gas sealed by a 26 m diameter flexible metal boot. The NaK pipe jackets are sealed to this wall by ceramic insulation and bellows fittings.

The intermediate heat exchangers are located in the guard band of the sodium pool such that the intermediate heat exchangers can move horizontally up to +/- 0.2 m with respect to the pool wall without any of the NaK pipes colliding with the pool wall to allow for relative thermal expansionand contraction.
 

VERTICAL ACCELERATION:
An important limiting factor is earthquake induced vertical acceleration. The fuel rods are held in position in the fuel tubes by gravity. If an earthquake produces a sudden upward acceleration greater than gravity followed by an immediate 1 g of gravitatinal acceleration the fuel rods could rise in their fuel tubes. The fuel tubes are in essence fixed to the Open Steel Lattice. Vertical movement of the opensteel lattice is damped by the liquid sodium pool. In this circumstance there is no certainty as to the relative positions of the movable and fixed fissile fuel rods, leading to potential for an accident. Thus any site that can potentially produce an earthquake induced vertical acceleration greater than 1 g should be rejected.
 

EARTHQUAKE OVERVIEW:
Severe earthquakes can cause short term horizontal oscillating ground accelerations of up to 3 g, although 1.25 g is a more practical design limit. The design approach taken herein is to design the FNR fuel bundles to resist normal crane handling stresses and to mount the fuel bundles in a fuel assembly supported by an open steel lattice on ball bearings such that if a severe earthquake occurs the fuel assembly, the open steel lattice and the immediately surrounding liquid sodium stay almost stationary while the primary sodium pool walls move with the surrounding ground. This objective is achieved by providing low friction bearings between the open steel lattice and the primary sodium pool bottom.

During an earthquake the primary liquid sodium will slosh around within the pool walls due to relative movement of the pool structure with respect to the primary liquid sodium. Removable 5 m high slosh guard panels will confine the liquid sodium for earthquake horizontal accelerations of up to 0.6 g.

The individual fuel tubes are protected from translational forces by the shroud plates and diagonal plates. However, on one side of the fuel assembly the shroud plates must exert force for vertical displacement the liquid sodium ahead of the fuel assembly.

The horizontal ground displacement during an earthquake can be expressed in the form:
(X - Xo) = A sin(W t)
Where;
Xo = initial horizontal position of the primary sodium pool with respect to the ground
X = primary sodium pool horizontal position as a function of time
A = maximum value of (X - Xo)
W = angular frequency of earthquake vibrations in radians / s
t = time

The velocity V is given by:
V = d(X - Xo) / dt
= W A cos(W t)

Hence the peak velocity Vp is given by:
Vp = W A

The horizontal ground acceleration Ah is given by:
Ah = dV / dt
= - W^2 A sin(W t)
= - [(W A)^2 / A] sin(W t)

Hence the peak horizontal ground acceleration Ahp is given by:
Ahp = [(W A)^2 / A]

Hence:
Ahp = Vp^2 / A
or
A = Vp^2 / Ahp

A violent earthquake is characterized by:
Ahp = 1.24 g
= 1.24 X 9.8 m / s^2
= 12.15 m / s^2
and by:
Vp = 1.16 m / s

Note that at a sustained 1.24 g horizontal acceleration the surface of the liquid sodium will be a more than 45 degrees to a horizontal reference.

Hence:
A = Vp^2 / Ahp
= [1.16 m / s]^2 / [12.15 m / s^2]
= 0.1107 m
which is a typical horizontal ground displacement.

Recall that:
W = Vp / A
or
F = Vp / (2 Pi A)
= (1.16 m / s) / [6.28 (0.1107 m)]
= 1.67 Hz

The liquid drag force F is given by:
F = K V^2

Thus the peak drag force Fp is given by:
Fp = K (W A)^2

Thus the intermediate heat exchanger bundles must be sufficiently robust to withstand a transverse liquid sodium flow rate of 1.16 m / s.

Thus in terms of drag force on the fuel assembly and intermediate heat exchange bundles we are concerned about the maximum horizontal ground velocity. The intermediate heat exchange bundles may need perforated cylindrical shields to limit the transvese drag forces on their heat exchange tubes.
 

POTENTIAL STANDING WAVES:
It is possible that there might be an issue with the natural surface wave resonant frequency of a 20 m diameter pool being excited by the earthquake frequency. The pool could be considered to be like a U tube where if the liquid rises on one side it falls on the other side. This system is in some respects like a pendulum. There is a kinetic enegy associated with the liquid sodium moving up and down. There is potential energy associated with one side of the pool being higher than the other side. A large slosh corresponds to a pendulum radius of 10 m. Smaller sloshes correspond to larger pendulum radii.
 

PENDULUM ANALYSIS:
Define:
Rp = pendulum length

Theta = pendulum angular deviation from vertical.

Pendulum KE = M V^2 / 2
= (M / 2) (Rp d(Theta) / dt)^2

H = fuel assembly center of mass height above its height when the pendulum is upright.

For small angles:
Pendulum PE = M g H = M g Rp Theta^2

Total Energy
= TE = KE + PE
= (M / 2) [Rp d(Theta) / dt]^2 + M g Rp Theta^2
= (M Rp / 2) [Rp (d(Theta) / dt)^2) + 2 g |Theta|]

Theta = B sin(Wp t)
Theta^2 = B^2 sin^2(Wp t)
dTheta / dt = B Wp cos (Wp t)
(d(Theta) / dt)^2 = B^2 Wp^2 cos^2(Wp t)
giving:
TE = (M Rp / 2) [Rp (d(Theta) / dt)^2) + 2 g Theta^2]
= (M Rp / 2) [Rp B^2 Wp^2 cos^2(Wp t) + 2 g B^2 sin^2(Wp t)]
= (M Rp / 2) B^2 2 g [(Rp Wp^2 / 2 g) cos^2(Wp t) + sin^2(Wp t)
]
= constant

Recall identity that:
cos^2(Wp t) + sin^2(Wp t) = 1

Hence:
Rp Wp^2 / 2 g = 1
or
Wp = [2 g / Rp]^0.5
or
Fp = (1 / 2 Pi)[2 g / Rp]^0.5
 

CAVITY RESONANT FREQUENCY RANGE:
For Rp = 20 m:
Fp = (1 / 2 Pi)[2 g / Rp]^0.5
= (1 / 6.28)[2 (9.8 m /s^2) / 20 m]^0.5
= 0.1576 Hz

For Rp = 10 m:
Fp = (1 / 2 Pi)[2 g / Rp]^0.5
= (1 / 6.28)[2 (9.8 m /s^2) / 10 m]^0.5
= 0.223 Hz

For Rp = 5 m:
Fp = (1 / 2 Pi)[2 g / Rp]^0.5
= (1 / 6.28)[2 (9.8 m /s^2) / 5 m]^0.5
= 0.315 Hz

Note that for severe earthquakes the cavity resonant frequency is much less than the earthquarke frequency. At low intensity earthquakes, where the earthquake frequency may be lower and periodic, we rely on the fuel bundles and the intermediate heat exchangers to provide sufficient primary sodium flow damping to prevent earthquake excited surface waves in the liquid sodium from growing.

Note that the pond will not support large waves at Rp > 10 m.

The FNR design set out herein must safely withstand a maximum horizontal ground velocity of 1.16 m / s.

EARTHQUAKE TOLERANCE:
FNRs must not be damaged by horizontal accelerations of up to 4.9 m / s^2 (0.5 g) and must not go prompt critical under the circumstances of the most violent recorded earthquakes involving horizontal ground shaking with accelerations up to 28 m / s^2 and velocities up to 1.2 m / s. This level of earthquake tolerance can be achieved by supporting the fuel assembly amd open steel lattice on low friction bearings such that their inertia attenuates horizontal forces on the fuel assembly. This bearing arrangement is discussed on the web pages titled FNR Open Steel Lattice and FNR Earthquake Protection.

When an earthquake wave is detected all the movable fuel bundles should immediately withdraw to reduce the reactor reactivity. The earthquake wave might be sufficient to cause a mechanical distortion in whch case it is essential that the movable fuel bundles be fully withdrawn at the time the distortion occurs.

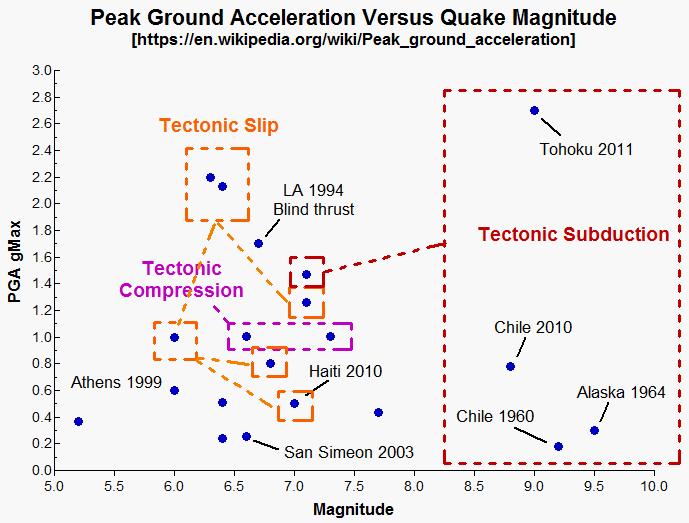
Here is a chart plotted by Dr. Alex Cannara of major recorded earthquakes.

With respect to reactor flexing in an earthquake one must think about reactor reactivity. If a reactor flexes away from its normal steady state geometry we need certainty that the reactivity will decrease, regardless of the direction of flexing. If that is not the case, during a severe earthquake the reactor could briefly flex into a prompt critical state. In a U-235 fuelled thermal neutron reactor brief flexing into prompt criticality is not the end of the world because the flexing period is usually less than one second, so the time in prompt criticality is usually not sufficient for a large growth in the number of neutrons, provided that formation of coolant voids does not inject positive reactivity.

However, in a Pu-239 fueled fast neutron reactor the margin between normal and prompt critical is only about one third that in a thermal neutron reactor and the rate of growth of neutrons in a prompt critical state is two orders of magnitude faster in a FNR than in a thermal neutron reactor. Thus it is important that any flexing reduce the reactor reactivity and as a backup there should be another mechanism to rapidly suppress prompt criticality.

There are two other stability mechanisms. One involves making the reactor short term power stable on fast neutrons independent of delayed neutrons. This is possible because the fuel temperature responds to prompt criticality faster than do the temperatures of the surrounding steel and sodium. The other involves fuel disassembly within fuel tubes which disassembly must operate within about 10^-4 seconds. ie The mechanical dynamics of separation of core fuel rods inside a fuel tube must be comparable to the dynamics of a bullet in a gun.

Ideally a fast neutron power reactor should be stabilized by all three mechanisms.

A fourth important mechanism is to give the FNR sufficient thermal mass that it can withstand a brief period of prompt criticality.

One of the possible issues with a sodium cooled reactor is positive reactivity injection by a sodium thermal expansion and ultimately sodium voids. We need to keep the reactor in a regime where sodium void formation is impossible. That may require a deeper sodium pool to maintain a sodium pressure head than would otherwise be necessary.
 

This web page last updated December 2,2023.