XYLENE POWER LTD.

FNR TEMPERATURE SETPOINT

By Charles Rhodes, P.Eng., Ph.D.

FNR TEMPERATURE SETPOINT To:
The fissile fuel of a FNR spontaneously maintains a average fuel temperature:
T = To
where To is known as the FNR's temperature setpoint.

The temperature setpoint To is a function of the FNR's nuclear fuel geometry. For practical reasons To is typically chosen to be:
To = 460 degrees C.

These reasons include:
a) Ability to tolerate long term reactor operation with two adjacent sodium cooling channel blockages which at full load can cause the local peak fuel temperature to go as high as 560 degrees C;
b) Keeping the peak temperature of the interior stainless steel cup which forms the primary sodium pool liner under 475 degrees C, at which temperature long term stainless steel phase changes commence.

The balance of this web page is primarily concerned about peak fuel temperature issues.

At average fuel temperature:
T = To
the FNR reactivity R is:
R = 0

As shown on the webpage titled: FNR REACTIVITY a requirement for FNR stablity is:
(dR / dT) < 0
at all accessible values of To.

The web page titled:FNR PRIMARY SODIUM FLOW develops the relationship between (Tpd - Tpi) and FNR thermal power P, where:
Tpd = fuel assembly primary sodium discharge temperature
and
Tpi = fuel assembly primary sodium inlet temperature
and
To ~ Tpd

This web page is primarily concerned with issues related to the FNR temperature setpoint To.
 

FNR DESIGN:
The instantaneous average temperature of a FNR is a cumulative result of its past fission heating and its past thermal load. At the operating point of a FNR:
(fission heating) = (thermal load)
and the average core zone fuel temperature of the FNR remains nearly constant at its temperature setpoint To.

At the FNR operating point the fission heat output must follow the relatively slowly varying thermal load. This load following requires that the number of free neutrons N in the FNR varies with the thermal load. If the thermal load falls to zero the fission heating must also fall to zero which means that N must fall to zero.

Recall that the web page FNR Reactivity gave the number of free neutrons N in a FNR as:
N = No Exp[R (t - to)]
where:
No = number of free neutrons in the FNR at time:
t = to
and
R = FNR reactivity

This for the FNR to function as outlined above:
If T > To then:
R < 0
and
if T < To
then:
R > 0.

This condition is realized in FNR design by making reactivity R satisfy:
[R|T = To] = 0
and
[dR / dT] < 0
for all accessible values of To.

That condition is realized by choice of suitable FNR geometry while taking into consideration the known thermal coefficients of expansion of the various FNR materials. The temperature setpoint To is adjusted by using a mechanical arrangement to make a small change to the FNR fuel geometry.

Then at:
To = 460 degrees C
R = 0
and
[dR / dT] < 0
which is the requirement for a stable FNR.

There are practical limits on the size of [dR / dT]. It is essential that the inequality
[dR / dT] < 0
remain satisfied over the entire range of possible FNR fissile fuel concentrations and fuel geometries. It is also essential that if To is adjusted that T follow it.
 

AVERAGE FUEL TEMPERATURE MAINTENANCE IN A FNR:
Consider a thermally controlled FNR operating at its temperature setpoint To. Its thermal load is constant. Its reactivity R is zero.

If part of that FNR is then further cooled by a fluid coolant thermal contraction increases the concentration of fissile atoms in the cooled portion of the FNR fuel. That contraction causes the FNR reactivity R to become greater than zero, thus causing a rapid growth in the number of free neutrons N. Provided that the fuel rod length is not so large as to prevent sharing of fission neutrons, this phenomena enables relatively uniform heat production in the fuel rod and smooth coolant temperature rise as it flows along the length of the fuel rod. The additional free neutrons quickly spread through the entire FNR and cause additional fissioning in uncooled regions of the FNR. The additional fissioning causes the temperature of the uncooled fuel regions to rise sufficiently above the average temperature setpoint To to reduce the FNR net reactivity R back to zero.

Thus a thermally controlled FNR has the remarkable property that, subject to geometric stability of its fuel assembly, it produces free neutrons which cause fission heating that maintains the FNR average fuel temperature at To independent of the thermal load. If one part of FNR fuel is fluid cooled another part of the fuel warms up to keep the average FNR fuel temperature T constant at T = To.

The FNR temperature setpoint To is a function of the FNR fuel geometry. A FNR is designed so that at all accessible values of To:
[dR / dT] < 0.

The reactivity R increases with increasing fissile atom concentration. However, due to fuel thermal expansion the fissile atom concentration decreases with increasing fuel temperature, causing:
{[dR / dT]|T = To} < 0
which causes:
[dTo / dT] < 0.

This feature gives the FNR power and temperature stability. When:
T < To
then:
R > 0
and the production of free neutrons causes fission heating which causes the FNR average temperature T to spontaneously rise.

When the temperature T reaches To:
T = To
and
R = 0
net heating stops and the FNR temperature cannot further rise because:
[dTo / dT] < 0

If:
T > To
then:
R < 0
which causes N to rapidly fall to zero which stops further fission heating. If there is a thermal load there is a net loss of heat from the FNR and the average FNR fuel temperature will fall to:
T = To
before fission heating can restart.
 

REAL FNR CORE FUEL ROD:
Suppose that we consider a round core fuel rod of uniform radius and uniform fissionable material within a FNR. Assume that the FNR fuel assembly is geometrically configured such that its temperature setpoint is:
To = 460 degrees C.

If the fuel rod material is initially all at 460 degrees C, the FNR temperature setpoint, the reactivity R = 0, there is no fission and hence the fuel rod emits no heat. This is the no load situation in a FNR.

Now assume that the outside surface of this fuel rod is uniformly cooled by a large bath of liquid sodium at 435 degrees C. Then the temperature of the fuel rod surface becomes 435 degrees C. The center line temperature of the fuel rod will instantly rise to 485 degrees C to keep the average fuel rod temperature To constant at:
To = 460 degrees C.
In these circumstances there is a 50 degree C temperature difference between the fuel rod center line and the fuel rod outside surface which will cause an ongoing radial heat flow from the fuel through the fuel rod outside surface and into the coolant.

Now assume that sodium flows along the fuel rod surface confined by a cooling channel. Assume that at the sodium inlet end of the fuel rod the outside surface of the fuel rod is further liquid sodium cooled by 25 degrees C from 435 degrees C to 410 degrees C. Then to maintain the fuel rod average temperature:
To = 460 degrees C
the fuel rod outside surface temperature at the sodium discharge end of the fuel rod will rise 25 degrees C from 435 degrees C to 460 degrees C.

Now at the a point equidistant from the ends of the fuel rod the average fuel rod temperature is 460 degrees C, the fuel rod surface temperature is 435 degrees C and the fuel rod centerline temperature is 485 degrees C.

Along the fuel rod center line the temperature near the sodium inlet is 460 degrees C, the temperature equidistant from the fuel rod ends is 485 C and the temperature at the hot end of the fuel rod is 510 degrees C.

At the radius from the fuel rod center line of the fuel rod average radial temperature the fuel rod temperature equidistant from the ends is 460 degrees C. At this same fuel rod radius at the sodium inlet end the temperature is 435 degrees C and at the sodium discharge end is 485 degrees C.

In a FNR at full load 410 degree C inlet sodium cools the outside surface of the fuel rods. The cooling sodium flows along the outside of the fuel rods absorbing heat and gaining temperature with distance at the same rate as does the outside surface temperature of the fuel rod. The cooling sodium discharges at the same temperature as the outside surface of the fuel rod at its discharge end, which temperature is 460 degrees C.
 

FNR NO LOAD OPERATION SUMMARY:
At no load the fuel rod centerline temperature is 460 degrees C at the sodium inlet end and is 460 degrees C at the sodium discharge end. Over the same distance the temperatures of both the fuel rod surface and the cooling sodium remain constant at 460 degrees C. At every point along the fuel rod there is a 0 degree C temperature difference between the fuel rod center line and the liquid sodium.
 

FNR NORMAL FULL LOAD OPERATION SUMMARY:
At full load the fuel rod centerline temperature rises from 460 degrees C at the sodium inlet end to 510 degrees C at the sodium discharge end. Over the same distance the temperatures of both the fuel rod surface and the cooling sodium rise from 410 degrees C to 460 degrees C. At every point along the fuel rod there is a 50 degree C temperature difference between the fuel rod center line and the liquid sodium.

A FNR normally operates such that when the primary coolant inlet temperature Tpi is less than the FNR setpoint temperature To the rate of free neutron generation exactly equals the rate of free neutron loss so that the FNR thermal power is constant. If the primary coolant inlet temperature Tpi decreases then N increases causing the reactor thermal power to increase and if the primary coolant inlet temperature Tpi increases then N decreases the reactor thermal power decreases.
 

OPERATING SUMMARY:
The FNR thermal power is proportional to both the coolant flow rate Fp and
(To - Tpi).
As long as Tpi < To the average fuel temperature To in a FNR remains constant. A FNR spontaneously varies its thermal power output to maintain a constant average fuel temperature To. In normal electricity generation applications setpoint To is kept constant and flow rate Fp is varied. Flow rate Fp is a natural circulation flow rate. However, due to the use a counter current heat exchange arrangement, Fp follows the secondary sodium flow rate Fs, which is mainly established by induction pumps. In the event of loss of station power the induction pumps will not operate, but the FNR secondary sodium system is designed to provide enough secondary sodium natural circulation to remove fission product decay heat.

The advantages of setting To and varying Fs include:
a) System safety;
b) Avoiding any need for primary sodium circulation pumps.

The advantage of fixing Fp and varying To as has been done by others is a lower value of (To - Tpi) and hence less thermal stress on the fuel assembly and intermediate heat exchange bumdles as the FNR changes its operating power level.
 

LOCAL TEMPERATURE RISE VARIATIONS:
A significant issue in FNRs is local variations in fuel rod temperature rise. In a FNR the concentration of free neutrons varies only slowly with position. However, the rate of heat generation in a core fuel rod is proportional to the product of the free neutron concentration and the fissile fuel atom concentration. Hence if core fuel rods in the same fuel bundle have significantly different fissile atom concentrations the heat output per fuel rod will be significantly different.

In a FNR with natural circulation of the primary sodium coolant an increased heat output per fuel rod due to a higher fissionable atom concentration causes an increase in liquid sodium flow past the fuel rod, so the change in sodium discharge temperature from fuel tube to fuel tube due to variations in fuel concentration is mitigated.

However, there is a potential complication that some primary sodium cooling channels might become partially obstructed as compared to other primary sodium cooling channels. Hence there can be significant local sodium discharge temperature variation resulting from sodium cooling channel obstruction. The effect of adjacent cooling channel cross section variations due to fuel tube warping tends to cancel. However, that is not the case if the cooling channel cross section variations are due to foreign particle obstruction.
 

BLOCKED COOLING CHANNELS:
In the FNR discussed herein each fuel tube has associated with it four sodium cooling channels. If two of those channels are obstructed the fission heat generated in the fuel will remain unchanged but the sodium coolant flow will be reduced by a factor of two. Hence the sodium temperature rise along the length of the fuel rod will double but the radial temperature drop within the fuel rod will remain the same. Hence the sodium discharge temperature will be:
410 degrees C + 2 (50 degrees C) = 510 degrees C
and the hottest point on the fuel rod centerline will reach:
510 degrees C + 50 degrees C = 560 degrees C
 

BLOCKED COOLING CHANNEL STATISTICS:
Assume that during the life of the reactor due to unforeseeable causes the primary sodium acquires a few particulates that are capable of blocking FNR cooling channels. Assume that the reactor has 300,000 cooling channels and that the reactor is in nearly constant operation. The probability of the first particulate blocking some cooling channel is 100%. The probability of the second particulate blocking a cooling channel adjacent to the first blocked channel is (4 / 300,000). The probability of the 3rd particulate blocking a cooling channel adjacent to the first two cooling channels is (6 / 300,000). Hence 2 blocking size particulates will not force a FNR shutdown but 3 blocking sixe particulates hava a:
(4 / 300,000)(6 / 300,000) = (24 / 9 X 10^10) = 1 chance in 3.75 billion of forcing a reactor shutdown.

Clearly it is important to do all necessary to minimize the number of potentially cooling channel size blocking particles that get into the primary sodium pool. It is also necessary to supply a filter with every active fuel bundle. The filter must stop potentially blocking particles but must not introduce signifcant flow resistance.
 

FINE ADJUSTMENT OF To:
The serpoint To is dependent on the FNR fisile fuel atom concentration and on the heating element geometry. The setpoint temperature To can be changed by changing the fuel assembly geometry.

During normal FNR operation, over a period of years, the FNR temperature setpoint To will gradually decrease due the long term changes in the FNR fissile fuel atom concentration. In order to keep
To = 460 degrees C
it is necessary to occasionally make small changes in the fuel geometry. These changes are achieved by small increases in the insertion of movable fuel bundles into the matrix of fixed fuel bundles.
 

GROSS ADJUSTMENT OF To
From time to time a FNR shutdown may be necessary to permit FNR refuelling and / or to replace an intermediate heat exchange bundle. In those circumstances a FNR cool shutdown is executed which means that To is reduced to:
To = 120 degrees C
which is a low enough temperature to permit robotic work in the primary pool enclosure while still being hot enough to prevent the liquid sodium from changing from its liquid to its solid state. When the reactor temperature T approaches 120 degrees C the reactor thermal load should be totally removed which will cause the fission power to drop to zero. Then the reactor should be left without a thermal load for about one week to allow natural decay of Na-24 in the primary sodium pool. Only then can robotic work in the primary sodium pool enclosure can commence.

The setpoint temperature To is changed by changing the reactor fuel geometry. The setpoint temperature To is only reduced when it is necessary to lower the temperature of the primary sodium pool.
 

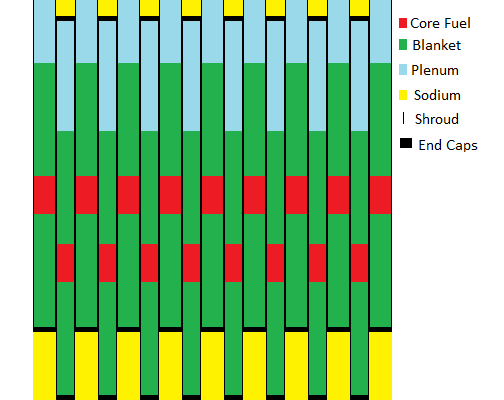
FUEL BUNDLE STATE DIAGRAM:
The insertion positions for a line of 8 movable fuel bundles inserted between 9 fixed fuel bundles are shown below for the cases of reactor cold shutdown, normal reactor operation and reactor at maximum possible power. In the reactor cold shutdown state the core rods (red) form two widely separated upper and lower core rod fuel concentration layers. In the normal reactor operating state the fixed and movable core rods partially overlap forming the core zone. As the fuel ages the amount of core rod overlap is gradually increased which increases the thickness of the core zone. When the fixed and movable core rods fully overlap the fuel bundles are ready to be removed for fission product decay cooling and then removal and reprocessing.
 

Reactor Cool Shutdown

 

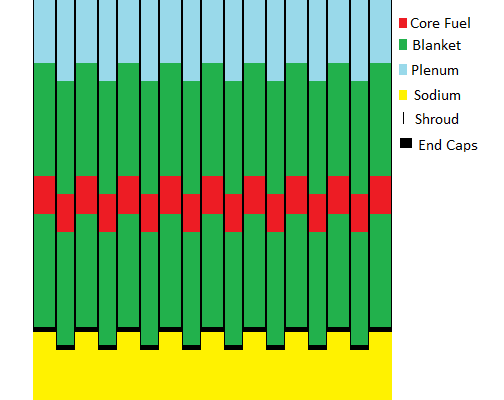Normal Reactor Operation

 

Reactor at Maximum Movable Fuel Bundle Insertion
 

Note that the maximum permitted vertical travel of a movable fuel bundle is 1.1 m which causes the transition between the movable fuel bundles fully withdrawn (reactor cold shut down) and movable fuel bundles fully inserted (maximum thermal power) states. Note that rapid over insertion of the movable fuel bundles into the matrix of fixed fuel bundles could potentially cause prompt neutron criticality.
 

FNR WARMUP:
When the work within the primary sodium pool enclosure is complete the setpoint temperature To can be slowly raised back to its normal value of:
To = 460 degrees C.

Define:
Tpi = FNR fuel bundle primary sodium inlet temperature

For a reactor intended to operate with:
(To - Tpi) < 50 degrees C
it is important on reactor warmup to slowly raise the fuel temperature setpoint To to gradually raise the temperature Tpi in the sodium pool so that the difference between To and Tpi never exceeds 50 degrees C.

It is easy to damage a FNR during primary sodium warm up by increasing To too quickly. The liquid sodium surface temperature as a function of time should plateau before the movable fuel bundle insertion depth is further increased.

During FNR warmup the moveable fuel bundles must be very slowly inserted into the matrix of fixed fuel bundles with no external thermal load to ensure that the peak fuel centerline temperature rating is not exceeded. This issue is particularly important when the fuel is new so the movable fuel bundle insertion distance is small which means that the available heat dissipation area on the core fuel tubes is also small.

In a practical FNR the large sodium pool should prevent a rapid change in temperature T. However, a practical FNR relies on an upper limit to the secondary sodium flow rate to prevent (To - T) in the primary sodium exceeding its rated value.

In order to sufficiently protect a FNR against damage during warm up it is necessary to recognize that the flow of primary liquid sodium coolant through a fuel bundle may not be uniform due to fuel bundle non-uniformity and due to potential obstruction of coolant channels by suspended particulate matter.

A matter of serious concern is the fuel center line temperature at its hot end which, if cooling channels are obstructed, can potentially exceed the material rating.
 

PROTECTION AGAINST A DEFECTIVE CONTROL SYSTEM:
In the event that due to a control system malfunction a new movable fuel bundle is erroneously driven toward its fully inserted state it is essential for the other movable fuel bundles, which are separately controlled, to immediately fully withdraw to cause a reactor cool shutdown.

When the fuel is new (average 20% Pu) and every second movable active fuel bundle is at its normal insertion depth while the remaining movable active fuel bundles are fully withdrawn the chain reaction must stop. This condition ensures that a cool shutdown condition is attainable with any one movable fuel bundle jammed in its normal operating position.

It is important to ensure that one isolated movable active fuel bundle with new fuel will not go prompt critical if it is accidentally fully inserted into the octagonal bundle matrix. As this circumstance is occurring the other independent shutdown system must instantly force a reactor cool shutdown. That cool shutdown will cause the four nearest neighbour movable fuel bundles to immediately fully withdraw. Hence, in all fuel conditions reactor prompt neutron criticality must be impossible if the four nearest neighbour movable active fuel bundles are fully withdrawn.

For clarity if the fixed fuel bundles are designated by F and the interlaced movable fuel bundles are grouped by A, B then in plan view:

ROW	FUEL BUNDLE TYPE
1	F A F A F A F A F A F A F A F A F A
2	B F B F B F B F B F B F B F B F B F
3	F A F A F A F A F A F A F A F A F A
4	B F B F B F B F B F B F B F B F B F

Note that each fixed fuel bundle F is surrounded by 2 X A and 2 X B with 4 fixed bundles on diagonals (except for the outer perimeter).
Note that each type A movable bundle is surrounded by 4 X F fixed bundles with 4 X B movable bundles on diagonals (except for the outer perimeter);
Note that each type B movable bundle is surrounded by 4 X F fixed bundles with 4 X A movable bundles on diagonals (except for the outer perimeter).

Note that A and B bundles occur in every second row and every second column.

Thus if any A bundle jams the four nearest B bundles are withdrawn to compensate. Similarly if any B bundle jams the four nearest A bundles are withdrawn to compensate.

Achieving certain reactor shutdown while allowing for the desired range of Pu-239 concentration decay in the core fuel rods likely requires a 1.1 m movable fuel bundle withdrawal. A 1.8 m blanket thickness is required to guarantee 1.2 m blanket thickness at times when there is almost no overlap between the fixed and movable core fuel rods. More typically the fuel bundle core rod overlap is 0.45 m resulting in a guaranteed 1.65 m blanket thickness.
 

THERMAL POWER:
The web page titled:FNR PRIMARY SODIUM FLOW develops the relationship between (Tpd - Tpi) and FNR thermal power P. It is shown that:
Tpd ~ To

The thermal resistance related to the fuel rods and fuel tubes in a FNR causes the FNR primary coolant discharge temperature Tpd to be less than the peak fuel rod center line temperature Tch at the hot end of the fuel rod. The temperature difference:
(Tch - Tpd)
increases with reactor thermal power. The thermal resistance is the combined effect of the finite thermal conductivities of the fuel rod, the sodium internal to the fuel tubes, the fuel tube wall and the sodium coolant boundary layer on the outside of the fuel tube wall.

However, the reactor thermal power P can also be expressed in terms of the coolant temperature rise in the form:
P = Fp Cp (Tpd - Tpi)
where:
Fp = primary coolant mass flow rate;
and
Cp = coolant heat capacity.

The import of this equation is that if there is a high primary coolant flow rate Fp, the temperature differential:
(Tpd - Tpi)
may have to be reduced to prevent the FNR's heating element thermal power rating being exceeded.

For a FNR which relies on natural primary sodium circulation this relationship indirectly sets the required number of active fuel tubes corresponding to a particular secondary sodium flow rate and temperature differential.
 

Note that as primary coolant flow rate Fp goes to zero then P goes to zero.

In the practical FNR described herein the secondary sodium flow rate Fs is controlled to limit the FNR thermal power. Hence the FNR converges to a steady state condition where the fission thermal power output equals the rate at which heat is removed by the coolant,
 

As shown on the web page FNR PRIMARY SODIUM FLOW RATE, in order to have sufficient primary sodium natural circulation at full thermal power we want to operate at:
P = 1000 MWt at:
Tpd = 460 C,
Tpi = 410 C

WARNING:
Historically in other liquid sodium cooled reactors there have been a number of cases of FNR fuel tube melting. It is important to realize that the nuclear reaction will deliver the instantaneous thermal power:
P = Fp Cp (Tpd - Tpi)

This thermal power is delivered by thermal conduction from the nuclear fuel througn the fuel tube walls and into the primary liquid sodium. The nuclear reaction is unaware that thermal power P can easily physically exceed the available thermal conduction heat transport capacity, thus causing fuel center line melting.

It is up to the FNR system designer to do all necessary to keep the thermal power P within the FNR physical material limits. A simple way to achieve that objective in normal FNR operation is to limit the the thermal power that can flow through the FNR's secondary heat transport loops. However, care must also be used during FNR warmup.

In simple language the nuclear reaction in a FNR supplies sufficient instantaneous thermal power to discharge sodium at temperature at To, irrespective of FNR material related heat transport limitations. If the system designer fails to do all necessary to limit the maximum value of:
P = Fp Cp (Tpd - Tpi)
or if reactor operators and/or service personnel defeat mechanisms designed to limit the maximum rate of change of:
To ~ Tpd
sooner or later the fuel heat transport capacity will be exceeded and the fuel and fuel tubes will be damaged.
 

SOURCE OF HISTORICAL FNR PROBLEMS:
Suppose that a historical FNR for some reason was shut down using its control rods. While in the off state the sodium pool gradually cooled. When the reactor was to be used again the control rods should have been withdrawn very slowly to gradually bring the sodium pool back to its design operating temperature. Too rapid withdrawal of the control rods would cause a FNR thermal power surge sufficient to damage the FNR fuel tubes.
 

OPERATING SUMMARY:
The FNR thermal power is proportional to both the coolant flow rate Fp and
(Tpd - Tpi).
A FNR spontaneously varies its thermal power output to maintain a constant average fuel temperature To, where: To ~ Tpd.
Flow rate Fp is a natural circulation flow rate which is a function of (To - Tpi).

In normal opertion reactor power P is limited by the heat transport rate through the secondary sodium heat transport loops which rate is established by induction pumps. In the event of loss of station power the induction pumps will not operate, but the FNR secondary sodium loops will provide enough secondary sodium natural circulation to remove fission product decay heat from the primary sodium.

The advantages of setting To and varying secondary sodium flow rate Fs include:
a) System safety;
b) Avoiding any need for primary sodium circulation pumps.
 

This web page last updated May 20, 2022.