XYLENE POWER LTD.

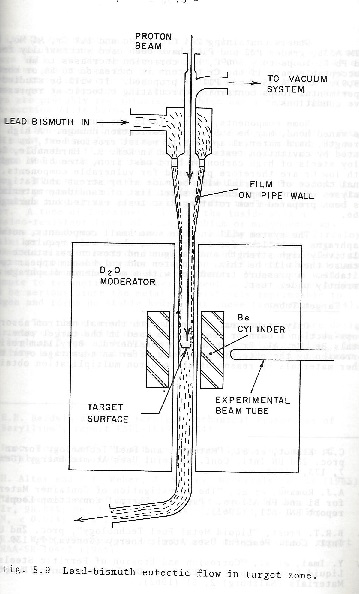
SIDE ELEVATION OF AN INTENSE NEUTRON GENERATOR:

APPLICATION:
An intense neutron generator has a multiplicity of scientific applications. However, with respect to Fast Neutron Reactors (FNRs) we are mainly concerned with using INGs to make TRU. TRU are atoms with atomic numbers greater than 92 that play a key role in FNR core fuel.
 

MAKING TRU:
TRU is made by exposing U-238 to a thermal neutron flux. Hence in the simplest implementation the ING heavy water tank is simply surrounded by U-238. However, the average TRU production can be approximately doubled by designing the U-238 blanket to act as a sub critical reactor. That reactor will dissipate substantial heat so the U-238 blanket then becomes a collection of U-238 in fuel tubes, similar to CANDU fuel bundles. The TRU will form in these fuel bundles. Harvesting the TRU is done in the same manner as recovering TRU from used CANDU fuel bundles.
 

COST:
An ING without a sub-critical blanket is an expensive way of making TRU. Typically, without a sub-critical blanket takes about:
1 GeV / (0.7 X 25) = 57 MeV
of electrical energy to make each TRU atom. However, when large scale deployment of FNRs is required there simply is not enough TRU available from used power reactor fuel to meet all the TRU requirements of FNRs. INGs must be used to meet much of the TRU requirement.
 

LONG TERM PLANNING:
Producing significant amounts of TRU with an ING is a slow process that requires years. Hence it is crucial to identify future TRU requirements decades in advance. Producing TRU requires a lot of electricity. The least expensive source of that electricity is surplus clean electricity that would otherwise be curtailed. However, the capacity factor of such electricity is seldom over 50%. That capacity factor further increases the time required to produce TRU.
 

ING WITH NO NEUTRON MULTIPLICATION IN BLANKET:
This material relates to the performance of the sub critical ING blanket.

The ING concept is to bombard flowing Pb-Bi eutectic with 1 GeV protons.

In the ING apparatus as designed by AECL each incident 1 GeV proton produces N = 25 free thermal neutrons that are then absorbed by a sub critical U-238 - TRU blanket to make more TRU atoms.

Assume am accelerator electrical efficiency of o.90.

We need to rate INGs in terms of g TRU / GWe-year of electricity in order to calculate the ING run time necessary to produce 20 tonnes of TRU as required for starting one 300 MWe FNR.

If an ING has no sub critical blanket for neutron multiplication:
TRU atom produced / net electrical energy output = (25 TRU atom X 0.90) / GeV
Now convert the ING output into g TRU / GWe-year:
25 TRU atom / proton X 239 g TRU / mole X 1 mole / 6.023 X 10^23 atoms = 992 X 10^-23 g TRU / proton

Then the gross electricity consumption per incident proton is: 1.0 GeV / 0.90 = 1.11 GeV / proton
[1.11 GeV / proton] X [10^9 eV / GeV] X [1.602 X 10^-19 J / eV] X [1W-s / J]X [1 h / 3600s ] X [1 year / 8766 h] X 1 GW / 10^9 W]
= [1.11 ] X [1.602 X 10^-25] X [1]X [1 / 3.600 ] X [1 year / 8.766 ] X [1 GW ]
= 0.0564 X 10-25 GW-year / proton

Then with no neutron multiplication in the U-238 blanket the TRU output per unit of gross electricity consumed is:
992 X10^-23 g TRU / 0.0564 X 10^-25 GW-year
= .992 X 10^-20 g TRU / 5.64 X 10^-27 GW-year
= 0.1759 X 10^7 g TRU/ GW-year
= 1.759 X 10^6 g TRU / GWe-year
= 1.759 tonnes / GWe-year

TRU output of a CANDU Reactor per unit of electricity generated is:
TRU Output = [4 g TRU / 1 GWe-years-kg] X 10^5 kg
= 4 X 10^5 g TRU / GWe-year
= 0.4 tonnes / GWE-year

Find the gross ING electric feed energy required to produce enough TRU to start a 300 MWe FNR:
Required TRU = 20 tonnes
The ING feed energy required to make this TRU with no blanket neutron multiplication is:
20 tonnes TRU / [1.759 tonnes TRU/ GWe-year]
= 11.37 GWe-year

If the ING is rated for an electricity input of 300 MWe = 0.300 GWe then the required ING run time to form enough TRU to start a 300 MWe FNR is:
11.37 GWe-year / 0.3 GWe
= 37.9 years

This period is too long.
 

ING WITH SUB CRITICAL BLANKET:
We must let TRU build up in the ING blankets and then run them as sub critical reactors to improve their thermal power output and to reduce their replication time at least two fold.
By doubling the neutron flux we can start with a 300 MWe ING and then every 19 years produce enough TRU to add another 300 MWe FNR.

Assume that a sub-critical blanket is fabricated such that for every generation of new neutrons (3 / 4) of the neutrons are absorbed by U-238 to make new TRU atoms and (1 / 4) of the neutrons cause fission of TRU atoms.
Assume that each TRU atom fission yields 3 free neutrons
Assume accelerator efficiency = 90%.
Gross electrical energy requirement per incident proton = 1 GeVe / 0.9 = 1.111 GeVe
Each incident 1 GeV proton produces 25 TRU atoms
Net electrical energy input per proton = 1.111 GeVe / 25
First neutron generation:
(3 N / 4) new TRU atoms
(N / 4) TRU atom fissions + (N / 4)(200 MeV)
(3 N / 4) second generation neutrons
(N / 2) net new TRU atoms

Second neutron generation:
(3 / 4)(3 N / 4) new TRU atoms
(1 / 4)(3 N / 4) TRU atom fissions + (1 / 4)(3 N / 4)(200 MeV)
(3 / 4)(3 N / 4) third generation neutrons
(1 / 2)(3 N / 4) net new TRU atoms

Third neutron generation:
(3 / 4)(3 / 4)(3 N /4) new TRU atoms
(1 / 4)(3 / 4)(3 N / 4) TRU atom fissions + (1 / 4)(3 / 4)(3 N / 4) (200 MeV)
(3 / 4)(3 / 4)(3 N / 4) fourth generation neutrons
(1 / 2)(3 / 4)(3 N / 4) net new TRU atoms

Fourth neutron generation:
(3 / 4)(3 / 4)(3 / 4)(3 N /4) new TRU atoms
(1 / 4)(3 / 4)(3 / 4)(3 N /4) TRU atom fissions + (1 / 4)(3 / 4)(3 / 4)(3 N /4)(200 MeV)
(3 / 4)(3 / 4)(3 / 4)(3 N /4) fifth generation neutrons
(1 / 2)(3 / 4)(3 / 4)(3 N /4) net new TRU atoms

Thus the net number of new TRU atoms formed per incident 1 GeV proton is:
(N / 2) + (1 / 2)(3 N / 4) + (1 / 2)(3 / 4)(3 N / 4) + (1 / 2)(3 / 4)(3 / 4)(3 N /4) + . . .
= (N / 2)(1) + (N / 2)(3 / 4)^1 + (N / 2)(3 / 4)^2 + (N / 2)(3 /4)^3 + . . .
= (N / 2)[1 + r + r^2 + r^3 +....] where r = (3 / 4)
= (N / 2) / (1-r)
= 2 N

Hence, for N = 25, the number of TRU atoms per energetic proton is:
2 X 25 = 50

For each incident 1 GeV proton the net fission power emitted by the blanket is:
(N / 4)(200 MeV) + (1 / 4)(3 N / 4)(200 MeV) + (1 / 4)(3 / 4)(3 N / 4) (200 MeV) + (1 / 4)(3 / 4)(3 / 4)(3 N /4)(200 MeV) + . . .
= (N / 4)(200 MeV)[1 + (3 / 4) + (3 / 4)^2 + (3 / 4)^3 + . . .]
= (N / 4)(200 MeV) / (1-r)
= N (200 MeV)

This output is heat. If converted into electricity it can supply N(200 MeV) / 3 per 1 GeV incident proton.
For N = 25 the available electricity is:
25 (0.2 GeV ) / 3 = 5 / 3 GeV
which is more than enough to power the proton accelerator.

In summary the contemplated ING apparatus with a sub critical blanket readily produces 50 TRU atoms per incident 1 GeV proton and each 1 GeV proton results in
1.11 GeV + 25 (200 MeV) = 6.11 GeV of heat dissipation.

Performing a units conversion gives:
50 TRU atom X 239 g / mole X 1 mole / 6.023 X 10^23 atoms = 1984 X 10^-23 g TRU

[6.11 GeV] X [10^9 eV / GeV] X [1.602 X 10^-19 J / eV] X [1W-s / J]X [1 h / 3600s ] X [1 year / 8766 h] X 1 GW / 10^9 W]
= [6.11 ] X [1.602 X 10^-25] X [1]X [1 / 3.600 ] X [1 year / 8.766 ] X [1 GW ]
= 0.3102 X 10-25 GW-year

Hence with an ING with a sub critical blanket the TRU formation rate can be expressed as:
1984 X 10^-23 g TRU / 0.3102 X 10-25 GWt-year
= 6.395 X 10^5 g TRU / GWt-year
= 0.6395 tonne TRU / GWt-year

TRU output of a CANDU Reactor
TRU Output = [4 g TRU / 3 GWt-years-kg] X 10^5 kg
= 1.333 X 10^5 g TRU / GWt-year
=0.1333 tonne TRU / GWt-year

Thus a 1 GWt rated CANDU reactor must run for:
[20 tonnes / GWt] / [0.1333 ton TRU /GWt-year]
= 150 years to directly produce enough TRU to start a new 1 GWt rated FNR.

Note that an ING, as described herein, in terms of heat dissipation is about:
[0.6395 tonne TRU / GWt-year] / [0.1333 tonne TRU / GWt-year]
= 4.8 X better than a CANDU at TRU production. The ING has the further advantage that it can start with no TRU. However, an ING needs time to form significant TRU inventory before it can act as a net energy source.
 

With a sub-critical ING blanket the ratio:
[Electricity Input/ proton] / [Heat output / proton]
= 1.11 GeV / [1.11 GeV + 25 (200 MeV)]
= 1.11 / 6.11
= 0.18167 GWe / GWt

Hence, a ING with a sub-critical blanket that outputs 1 GWt of heat requires an electricity input of about 181.67 MWe.

The corresponding net practical ING electricity generation is:
{[1 GWt / 3] - 181.67 GWe} / GWt
= 151.66 MWe / GWt
 

Consider two X 1 GWt INGs running in parallel, each with thermal to electric feedback. Net electricity output = 2 X 151.66 MWe = 391.32 MWe
TRU production = 2 X .6395 tonne TRU / year = 1.279 tonne / year
Run time required to make sufficient TRU to start a 1 GWt FNR:
= 20 tonnes / [1.279 tonne / year]
= 15.6 years

Thus with this equipment combination:
During the first 16 year period net electricity output with 2 INGs = 300 MW;
During the second 16 year period net electricity output with 2 INGs + 1 FNR = 600 MW;
During the third 16 year period net electricity output with 2 INGs + 2 FNR = 900 MW;
During the fourth 16 year period net electricity output With 2 INGs + 3 FNR = 1200 MW;
During the fifth 16 year period net electricity output with 2 INGs + 4 FNR = 1500 MW;

Note: Each ING envisaged herein is essentially 3 AECL INGs operating in parallel.
 

COST OF ING PRODUCED TRU AT $0.10 / kWeh:
In essence a 1 GWt ING uses half of its available output to produce TRU.
(0.187.67 GWe / GWt) / [0.6395 tonne TRU / GWt-year]
= [0.18767 GWe-year / 0.6395 tonne TRU]
= [0.18767 GWe-year / 0.6395 tonne TRU] X [$0.10 / kWeh] X [8766 h / year] X [10^6 kWe / GWe]
= $293.4 X 10^6 / tonne TRU
Clearly ING produced TRU significantly increases the cost of a FNR. Additional work is required to further improve the neutron gain of the ING and its sub-critical blanket. Viewed another way, used CANDU fuel contains TRU with an enormous potential value.
 

REFERENCES:

The Intense Neutron Generator DL-72 by W.B.Lewis, October 1966 AECL-2818

ING Status Report July 1967 AECL-2750

The Intense Neutron Generator and Future Factory Type Ion Accelerators DL-94 by W.B.Lewis, October 1968 AECL-3190
 

This web page last updated February 27, 2024